论文阅读笔记Do Transformers Really Perform Bad for Graph Representation
论文阅读笔记Do Transformers Really Perform Bad for Graph Representation
# 问题
Transformer在自然语言中效果好,在图上表现不好。
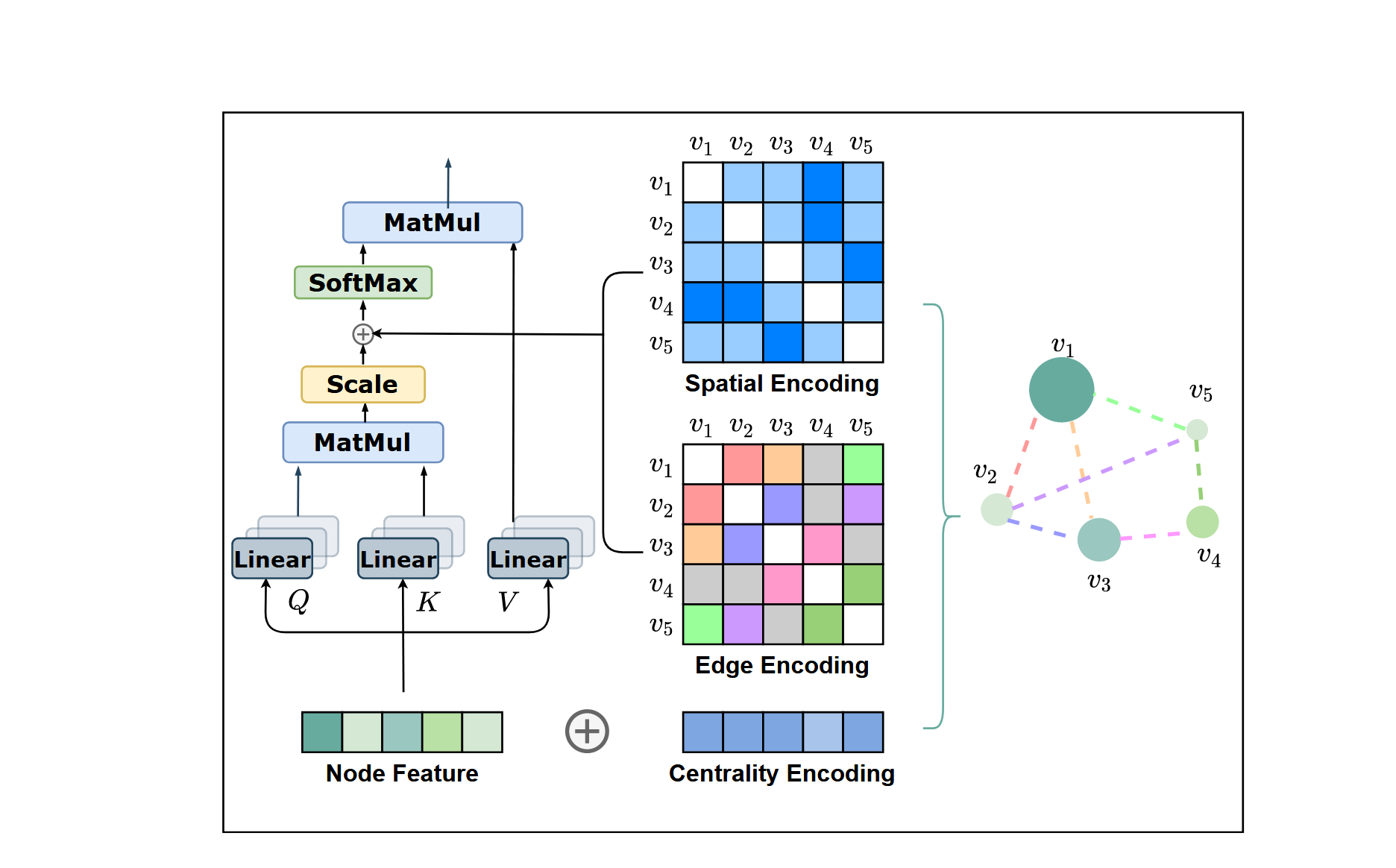
# 结构编码
# 1.节点中心性编码
传统transformer的注意力公式中,根据单词之间的相似性分配attention distribution,例如当前要翻译的是“猫在吃鱼”,模型在翻译“吃”这个词时,会计算它与“猫”、“鱼”等词的语义关联。如果“吃”和“鱼”的语义关联较强,那么attention机制会为“鱼”分配较高的注意力权重,帮助模型正确理解和翻译这个短语。
对于图来说,可以把每个节点的度中心性编码,如果是有向图则再细分为入度和出度中心性,然后和点的原始特征做加法,作为新的点的特征。
# 2.节点位置编码
Transformer模型的一个优势是其全局感受野。在每个Transformer层中,每个标记(token)都可以关注序列中任意位置的信息,并基于此信息处理其表示。但是,这种操作带来了一个附带问题:模型必须显式地指定token的位置,加入位置编码。
然而,对于图结构数据来说,节点并不像序列那样按顺序排列。为了在模型中编码图的结构信息,作者提出了一种新的空间编码(Spatial Encoding)方法。
对于顺序数据,可以采用两种方式来处理位置编码:
绝对位置编码(absolute positional encoding):为序列中的每个位置生成一个位置嵌入,这些嵌入作为输入传递给模型。这样,模型就知道每个元素在序列中的具体位置。比如位置1的元素、位置2的元素等都有明确的位置信息。
相对位置编码(relative positional encoding):这种方式不依赖于具体的位置,而是编码序列中任意两个位置之间的相对距离。通过这种方式,模型可以知道不同元素之间的相对顺序关系,而不必依赖绝对位置。
在本文中,考虑使用相对位置编码,考虑节点u和v,如果两个节点连通,则
令
这里
其中
# 3. 边编码
在很多图任务中,边也具有结构特征。
两种常见的边编码方法,一是将边的特征与其关联的节点特征相加,这样边的特征被直接传递给相关节点。二是在每个节点的特征聚合过程中,将与该节点相连的边的特征与节点特征一同使用。
这两种方法的共同问题是,边的信息只被传播到与边直接关联的节点。这意味着边特征没有很好地在整个图结构中得到传播或利用,从而限制了边特征在全图表示中的有效性。
为了更好地将边的特征编码到注意力机制中,Graphormer提出了一种新的边编码方法。
注意力机制中的节点相关性计算:在自注意力机制中,模型需要为每对节点
计算它们之间的相关性。传统方法只根据节点特征计算相关性,但Graphormer认为连接节点的边也应该被纳入相关性的计算中,因为边在节点之间的关系上起到了关键作用。 最短路径(Shortest Path)和边特征的引入:对于每对节点
,我们找到连接它们的最短路径 ,即从 到 的边序列。然后,计算路径上所有边特征与一个可学习的嵌入向量的点积,并取这些点积的平均值。这就相当于将沿着节点对之间的边的信息以一种加权平均的形式整合起来。 注意力机制中的修正:在自注意力机制中,注意力矩阵
的元素 通常通过节点特征的点积来计算。Graphormer引入了两项修正: 第一项是基于最短路径的空间编码
。 第二项是新的边特征编码
,具体定义如下: 其中,
是通过沿着最短路径上的每条边计算边特征与可学习的嵌入向量的点积,公式为: 这里,
是最短路径上第 条边的特征, 是对应的可学习权重嵌入, 是边特征的维度。